Logical Reasoning Explained: From Deduction to Abduction in Everyday Thinking
- THE MAG POST

- Sep 8
- 3 min read
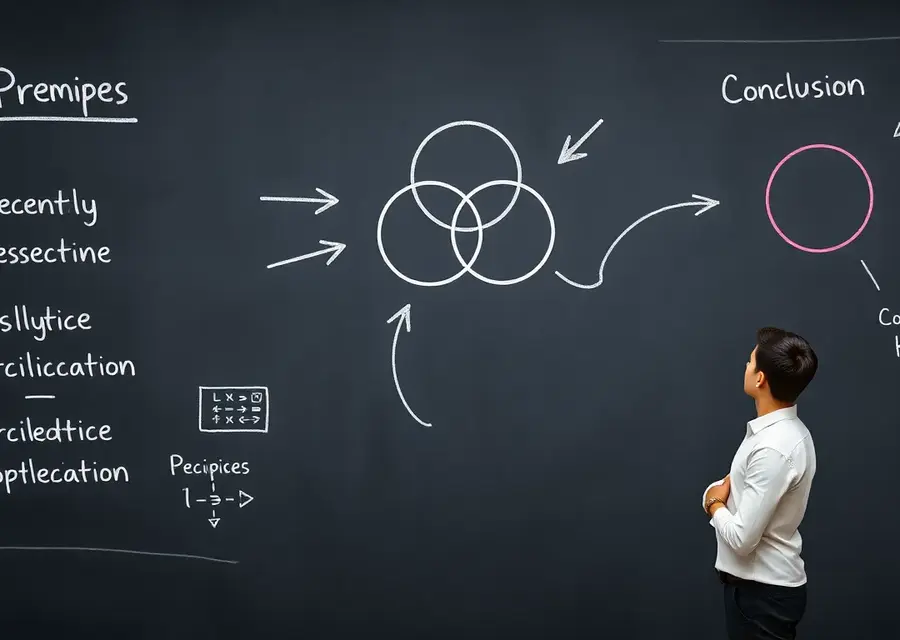
Logical reasoning explained reveals how we move from premises to conclusions with rigor and clarity. It distinguishes tight deductive proof from broader, probabilistic inference, showing when arguments are airtight and when they rest on evidence, assumptions, or uncertainty. This distinction matters in math, science, and everyday thinking.
By revisiting classic examples and contemporary challenges—ranging from formal proofs to diagnostic reasoning—we'll see how norms of inference govern credibility, why some conclusions are defensible, and how new information can shift an argument's standing. The goal is a practical literacy that respects nuance while rewarding precision.
Foundations of Logical Reasoning
Crucial to any rigorous argument is a clear map from premises to conclusions. Foundations of logical reasoning anchor how we assess that map in mathematics, science, and daily life.
Premises and Conclusions
A premise is a starting claim; the conclusion is what follows when we connect premises via an inference rule. In analytic work, both premises and conclusions are propositions—truth-valued statements about what is the case. The strength of an argument rests on how well premises support the conclusion.
In well-structured reasoning, the conclusion cannot be false if the premises are true; this captures the essence of deductive validity. The reliability of a conclusion then hinges on the correctness of the premises and the appropriateness of the inference used to link them.
Norms of Inference
Inference rules—templates like modus ponens or modus tollens—govern how we move from premises to conclusions. These norms are not arbitrary; they preserve truth across valid transformations and ensure arguments are scrutinizable rather than persuasive by rhetoric alone.
Different traditions emphasize various norms, from classical syllogisms to contemporary modal or temporal logics. The throughline is clear: premises must support conclusions in a way that can be tested, debated, and extended, not merely believed based on authority or sentiment.
Deduction and Its Counterparts
Deductive reasoning offers a distinctive form of certainty within a truth-preserving framework; it is the gold standard in formal systems and mathematics.
Deductive Certainty
A deductive argument is sound when it is valid and all its premises are true. Under a valid form, the conclusion follows necessarily from the premises. For example, if all humans are mortal and Socrates is a human, then Socrates is mortal—regardless of any other claims about reality.
Importantly, validity concerns form, not the factual accuracy of premises. A valid structure can exist even if one premise is false. This distinction clarifies why mathematics relies on deductive rigor and why scrutinizing premises is essential to sound reasoning.
Non-Deductive Reasoning in Practice
Non-deductive reasoning builds plausible conclusions from available evidence without guaranteeing truth. Inductive generalizations, abductive explanations, and analogies extend knowledge, yet their conclusions are defeasible—they may be revised in light of new data or counterexamples.
In daily life and science alike, abductive reasoning selects the best explanation among candidates, while induction generalizes from observed instances. Analogy transfers insight between similar systems. Each form enriches understanding, but none provides the certainty that strict deduction affords.
Applications and Pitfalls
Beyond theory, logical reasoning guides experiments, debates, and decisions under uncertainty. Distinguishing when to rely on deductive guarantees and when to hedge with probabilistic support is essential for sound judgment.
Everyday Reasoning and Science
Everyday reasoning often leans on induction: numerous observations prompt general claims. In science, large, representative samples and replicable tests curb bias and strengthen generalizations, while acknowledging the problem of induction reminds us that future data can shift current conclusions.
Crucial evidence comes from transparent premises, robust experimentation, and reproducible results. Clear articulation of assumptions and methods enhances credibility and informs policy, education, and public discourse.
Common Fallacies and Defenses
Fallacies arise when argument form or content misleads. Formal fallacies distort structure; informal fallacies exploit vagueness, false dilemmas, or misrepresented views. Recognizing patterns helps restore integrity by clarifying what is actually supported by evidence.
Defensive moves include clarifying premises, distinguishing correlation from causation, and avoiding overgeneralization. By making assumptions explicit and inviting scrutiny, reasoning becomes more robust and less susceptible to manipulation.
Key Takeaways
Logical reasoning explained emphasizes the spectrum from airtight deduction to probabilistic inference, clarifying when conclusions are guaranteed and when they are provisional. The discipline also trains us to spot fallacies, weigh evidence, and refine arguments for clarity and rigor.
Aspect | Summary |
What is logical reasoning | Moving from premises to conclusions using normative standards of inference. |
Deductive vs Non-Deductive | Deduction yields certainty; non-deduction yields probabilistic conclusions. |
Common types | Inductive, abductive, and analogical reasoning with caveats. |
Fallacies | Distinguishing formal and informal fallacies and how to counter them. |
Practical relevance | Role in critical thinking, science, and decision making with transparent premises. |















































Comments